Bài toán đã làm khó vô số người tham gia giải đố. Thậm chí nhiều người còn bảo: “Giải được đúng là thiên tài!”

Bài toán

Hai ông bà Lars cùng đến một buổi gặp mặt với 4 cặp vợ chồng khác nhân dịp năm mới. 5 cặp vợ chồng bắt tay nhau, nhưng không ai bắt tay chính vợ/chồng của mình. Sau khi bắt tay, ông Lars đến hỏi từng người xem họ bắt tay với bao nhiêu người.

Tất cả đều trả lời trung thực và thật ngạc nhiên là mỗi người lại đưa ra một câu trả lời khác nhau. Hỏi vợ chồng ông bà Lars bắt tay với bao nhiêu người?

Giả thiết

Trước tiên, hãy cùng xem một ví dụ nhỏ hơn để hiểu logic của bài toán này.

Hãy tưởng tượng một cuộc gặp gỡ nhỏ hơn giữa ông bà Lars và một cặp vợ chồng khác. Nhóm có tổng cộng 4 người. Vì không ai bắt tay người bạn đời của mình và không ai bắt tay người đó, mỗi người có thể bắt tay với 0, 1 hoặc 2 người. Nếu ông Lars nghe 3 câu trả lời khác nhau từ 3 người mà ông hỏi, thì mỗi người đưa ra một trong 3 câu trả lời có thể.

Người bắt tay với 2 người khác phải bắt tay với mọi người, trừ người bạn đời của mình. Điều này ngụ ý tất cả những người khác trong cuộc gặp mặt này sẽ bắt tay với ít nhất 1 người. Người duy nhất có thể trả lời 0 là người không thể bắt tay với người trả lời 2. Câu trả lời của 2 và 0 được ghép nối và thuộc về cặp vợ chồng kia.

Theo quy trình loại bỏ, câu trả lời 1 phải là bà Lars. Do đó, bà Lars bắt tay 1 người.

Còn ông Lars thì sao? Ông ta bắt tay với người trả lời 2, và vì không thể bắt tay với người vợ đã trả lời 1, đồng thời không thể bắt tay với người trả lời 0. Do đó, anh Lars phải bắt tay với 1 người, giống hệt vợ anh.

Phương pháp đồ họa (1 cặp đôi khác)

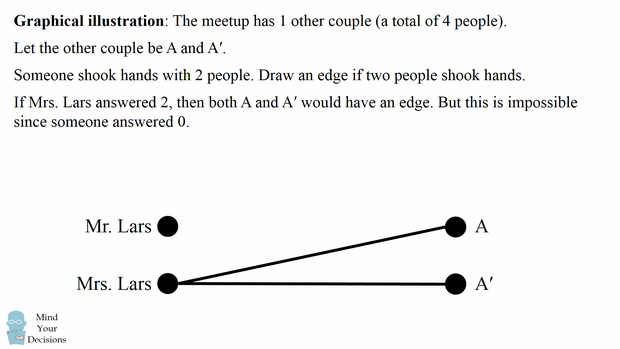
Chúng ta có thể vẽ 4 điểm cho nhóm người nói trên và có thể vẽ một cạnh giữa hai điểm nếu hai người bắt tay nhau. Ta sẽ dán nhãn cho ông bà Lars và sau đó gọi cặp vợ chồng khác là A và A ‘.

Một người trả lời 2, nghĩa là một số điểm có 2 cạnh. Nếu chúng ta vẽ 2 cạnh từ bà Lars, thì cả hai điểm khác sẽ kết nối với nhau bằng một cạnh. Nhưng điều này là không thể vì một người trả lời 0.

Do đó, để thực hiện được phải là một trong những điểm khác được kết nối bởi 2 cạnh. Vì người đó không thể kết nối với vợ/chồng của mình, 2 cạnh phải kết nối với ông bà Lars.

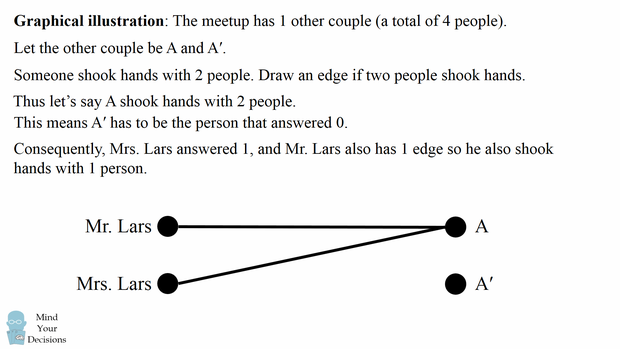
Từ biểu đồ này, chỉ có một điểm không được kết nối bởi đường thẳng nào. Đây là người vợ/chồng của người trả lời 2. Đây cũng là lựa chọn khả dụng duy nhất cho người trả lời 0. Do đó, những người trả lời 2 và 0 là một cặp.

Hơn nữa, chúng ta có thể thấy cả Bà và Ông Lars đều có một đường nối, vì vậy mỗi người trong số họ bắt tay với đúng 1 người.

Đáp án

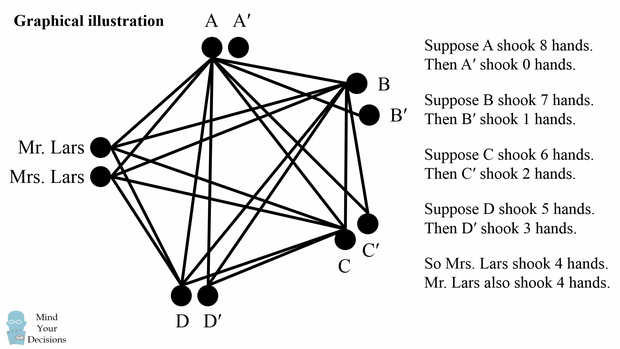
Tương tự với giải thiết trường hợp bên trên. Chúng ta có 10 người trong nhóm và mỗi người có thể bắt tay với 0, 1, 2, 3, 4, 5, 6, 7 hoặc 8 người.

Người bắt tay với 8 người bắt tay với tất cả mọi người ngoại trừ người bạn đời của chính mình. Vì mọi người khác bắt tay với ít nhất 1 người, điều đó có nghĩa là vợ/chồng của người này phải là người bắt tay với người trả lời là 0. Câu trả lời của 8 và 0 được ghép nối, và đây là một cặp vợ chồng.

Một số người khác bắt tay với 7 người, có nghĩa là bắt tay với tất cả mọi người ngoại trừ người vợ/chồng của chính họ và người trả lời 0. Bây giờ mọi người khác, ngoại trừ bạn đời và người trả lời 0, phải bắt tay với ít nhất 2 người, nghĩa là vợ/chồng của người đó phải là người bắt tay với 1 người. Câu trả lời của 7 và 1 được ghép nối, và đây là một cặp vợ chồng.

Logic tương tự có thể được tiếp tục cho thấy rằng câu trả lời của 6 và 2 là một cặp vợ chồng, cũng như câu trả lời của 5 và 3. Theo phương pháp loại trừ, câu trả lời còn lại phải là câu trả lời của bà Lars, người đã bắt tay với 4 người.

Còn ông Lars thì sao? Ông sẽ bắt tay với những người đưa ra câu trả lời 8, 7, 6 và 5. Ông ta không thể bắt tay với người trả lời 4 (vợ anh ta). Câu trả lời 3 bắt tay với câu trả lời 8, 7 và 6; câu trả lời 2 bắt tay với câu trả lời 8 và 7; và câu trả lời của 1 bắt tay với câu trả lời là 8. Câu trả lời 0 không bắt tay ai. Do đó, ông Lars bắt tay với đúng 4 người, giống như vợ mình.